การจำแนกประเภทเป็นปัญหาสำคัญในข้อมูลขนาดใหญ่วิทยาศาสตร์ข้อมูลและการเรียนรู้ของเครื่อง เพื่อนบ้านที่ใกล้ที่สุด K-K (KNN) เป็นหนึ่งในอัลกอริทึมที่เก่าแก่ที่สุด, ง่ายที่สุดและแม่นยำสำหรับการจำแนกรูปแบบและแบบจำลองการถดถอย KNN ถูกเสนอในปี 1951 โดย Fix, E. and Hodges, J.L. และแก้ไขโดย Cover, T., & Hart, P.
KNN ถูกระบุว่าเป็นหนึ่งในวิธีการจำแนกทีดีที่สุด 10 อันดับแรก ดังนั้น KNN ได้รับการศึกษาในช่วงไม่กี่ทศวรรษที่ผ่านมาและนำไปใช้อย่างกว้างขวางในหลาย ๆ วงการ ดังนั้น KNN จึงประกอบด้วยตัวจําแนกพื้นฐานในปัญหาการจําแนกรูปแบบหลายอย่างเช่นการจัดหมวดหมู่ข้อความ, โมเดลการจัดอันดับ, การรับรู้วัตถุ, และการรู้จำเหตุการณ์ เป็นต้น
การใช้งาน KNN เป็นอัลกอริธึมที่ไม่ใช้พารามิเตอร์ คำว่าไม่ใช้พารามิเตอร์หมายถึงไม่มีพารามิเตอร์หรือจำนวนพารามิเตอร์คงที่โดยไม่คำนึงถึงขนาดของข้อมูล แต่พารามิเตอร์จะถูกกำหนดโดยขนาดของชุดข้อมูลการฝึกสอน
K-nearest neighborhood (K-NN) เป็นการเรียนรู้ที่ดีมากต่อเทคนิคการจำแนกแบบ nonparametric และ parametric และมีประสิทธิภาพมากเมื่อใช้กับข้อมูลการสอนที่ใช้ฐานข้อมูลที่มาก การจำแนกโดยการใช้ K-nearest neighborhood (K-NN) เป็นตัวเลือกที่ดี ในวิธี nearest neighborhood เป็นความจำเป็นต่อการกำหนดค่าพารามิเตอร์ อันซึ่ง เป็นจำนวนของคุณลักษณะเด่นที่ใกล้เคียง
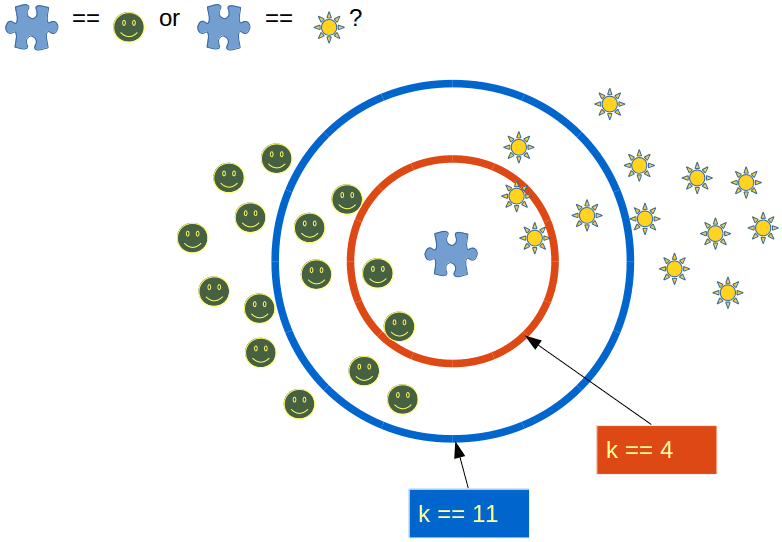
ขั้นตอนของ K-NN Imputation มี 3 ขั้นตอนดังนี้
ขั้นที่ 1: เลือก K ยีน ที่ใกล้ที่สุดกับยีนที่มี Missing Values (MV) เพื่อที่จะ Estimate Missing Values xij ของยีนที่ i-th ในตัวอย่างที่ ยีนซึ่งเป็น Expression Vector จะถูกเลือกโดย มีลักษณะการแสดงออกทางพันธุศาสตร์ i มากกว่า ตัวอย่าง j
ขั้นที่ 2: คำนวณหาระยะห่างระหว่างข้อมูล 2 Expression Vector xi และ xj ด้วยวิธีการ Euclidian distance ครอบคลุมส่วนประกอบต่างๆ ในตัวอย่าง j-th Euclidian distance ระหว่าง xi และ xj สามารถคำนวณได้จาก

โดยที่
d(xi,xj) คือ ระยะห่างระหว่างตัวอย่าง กับตัวอย่าง
n คือ จำนวนคุณสมบัติทั้งหมดของตัวอย่าง
xik คือ คุณสมบัติตัวที่ k ของตัวอย่าง
xjk คือ คุณสมบัติตัวที่ k ของตัวอย่าง

ขั้นที่ 3: เลือกค่าข้อมูลที่มีค่า dist น้อยที่สุด k ตัวเพื่อนำมาพิจารณาหาคำตอบ
สำหรับขั้นตอนในการเขียนโค๊ดใน Matlab เราก็จะเขียนตามสูตรข้างบนเลย
1. กำหนดข้อมูลการทดสอบ
dataMatrix = test; % ข้อมูลการทดสอบ
2. กำหนดข้อมูลการสอน
queryMatrix = datatraining; % ข้อมูลการสอน
3. % กำหนด k = 1
kn = 1; % กำหนด k = 1
4. กำหนดตัวแปรต่างๆให้เป็นเอาท์พุต
neighborIds = zeros(size(queryMatrix,1),kn); % กำหนดตัวแปร neighborIds ให้เป็นเอาท์พุต
neighborDistances = neighborIds; % กำหนดตัวแปร neighborDistances ให้เท่ากับ %neighborIds และให้เป็นเอาท์พุต
numDataVectors = size(dataMatrix,1); % กำหนดตัวแปร numDataVectors ให้เป็นเอาท์พุต
numQueryVectors = size(queryMatrix,1); % กำหนดตัวแปร numQueryVectors ให้เป็นเอาท์พุต
5. ทำการหาระยะทางจากสูตรข้างบน
for i=1:numQueryVectors, % วนลูปจนครบข้อมูลการสอน
dist = sum((repmat(queryMatrix(i,:),numDataVectors,1)-dataMatrix).²,2); % ทำการหาระยะทางระหว่างข้อมูลทดสอบกับข้อมูลการสอน โดยใช้สูตรที่ 1 แต่ยังไม่หา sqrt
[sortval sortpos] = sort(dist,’ascend’); % ทำการเรียงข้อมูลจากน้อยไปมาก
neighborIds(i,:) = sortpos(1:kn); % ทำการเรียงตำแหน่งของ pixel จากน้อยไปมาก
neighborDistances(i,:) = sqrt(sortval(1:kn)); % ทำการหา Sqrt
end
6. หาค่าที่ต่ำที่สุด
mini = min(neighborDistances);
7. % หาตำแหน่งที่ให้ค่าที่ต่ำที่สุด
out(iCentroid) = find(neighborDistances == mini);
หมายเหตุท้าย:
หากคุณชอบบทความนี้อย่าลืมคลิก❤ด้านล่างเพื่อแนะนำและถ้าคุณมีคำถามใด ๆ แสดงความคิดเห็นและฉันจะพยายามอย่างดีที่สุดที่จะตอบ คุณสามารถติดตามฉันบน facebook page (https://www.facebook.com/nextsoftwarehousethailand/) และสามารถส่งอีเมลถึงฉัน
ขอให้ทุกคนมีวันที่ดี 🙂